Introducción http://colos.inf.um.es/rlab/tutorial_es/Circuitos.html
http://www.plusformacion.com/Recursos/r/Teoria-basica-problemas-propuestos-circuitos-electricos-corriente-continua?quicktabs_ofertas_relacionadas_quicktab=2#ley
Se introduce en este apartado lo que se entiende por circuito eléctrico y la terminología y conceptos básicos necesarios para su estudio.
http://www.plusformacion.com/Recursos/r/Teoria-basica-problemas-propuestos-circuitos-electricos-corriente-continua?quicktabs_ofertas_relacionadas_quicktab=2#ley
Se introduce en este apartado lo que se entiende por circuito eléctrico y la terminología y conceptos básicos necesarios para su estudio.
Circuitos Eléctricos.
Un circuito eléctrico está compuesto normalmente por un conjunto de elementos activos -que generan energía eléctrica (por ejemplo baterías, que convierten la energía de tipo químico en eléctrica)- y de elementos pasivos -que consumen dicha energía (por ejemplo resistencias, que convierten la energía eléctrica en calor, por efecto Joule)- conectados entre sí.
El esquema siguiente presenta un circuito compuesto por una batería (elemento de la izquierda) y varias resistencias.
El esquema siguiente presenta un circuito compuesto por una batería (elemento de la izquierda) y varias resistencias.
Las magnitudes que se utilizan para describir el comportamiento de un circuito son
Estas magnitudes suelen representarse, respectivamente, por I y V y se miden en Amperios (A) y Voltios (V) en el Sistema Internacional de Unidades.
La intensidad de corriente eléctrica es la cantidad de carga que, por segundo, pasa a través de un cable o elemento de un circuito.
El voltaje es una medida de la separación o gradiente de cargas que se establece en un elemento del circuito. También se denomina caída de potencial o diferencia de potencial (d.d.p.) y, en general, se puede definir entre dos puntos arbitrarios de un circuito.
El voltaje está relacionado con la cantidad de energía que se convierte de eléctrica en otro tipo (calor en una resistencia) cuando pasa la unidad de carga por el dispositivo que se considere; se denomina fuerza electromotriz (f.e.m.) cuando se refiere al efecto contrario, conversión de energía de otro tipo (por ejemplo químico en una batería) en energía eléctrica.
La f.e.m. suele designarse por e y, lógicamente, se mide también en Voltios.
La f.e.m. suele designarse por e y, lógicamente, se mide también en Voltios.
Los elementos de un circuito se interconectan mediante conductores. Los conductores o cables metálicos se utilizan básicamente para conectar puntos que se desea estén al mismo potencial (es decir, idealmente la caída de potencial a lo largo de un cable o conductor metálico es cero).
Consideraciones Energéticas:
Según lo expuesto anteriormente, La energía que se convierte en otro tipo de energía cuando pasa una cierta cantidad de carga Q por un elemento pasivo es Q.V si es V la d.d.p. entre los extremos del dispositivo.
Al ser la corriente una medida de la cantidad de carga que pasa por segundo, la energía que por segundo se consumirá en el dispositivo será I.V; esta energía por unidad de tiempo esla Potencia.
Al ser la corriente una medida de la cantidad de carga que pasa por segundo, la energía que por segundo se consumirá en el dispositivo será I.V; esta energía por unidad de tiempo es
De igual forma, cuando consideramos elementos activos, la potencia eléctrica que dan cuando suministran una cierta corriente I será: e.I.
Es de destacar que en un dispositivo pasivo la corriente va en el sentido de los potenciales decrecientes (de + a -) mientras que en una batería ocurre lo contrario, la corriente va en el sentido de los potenciales crecientes (de – a +).
Esta distinción es la que determina que un elemento sea activo (produzca energía eléctrica) o sea pasivo (consuma energía eléctrica).
Esta distinción es la que determina que un elemento sea activo (produzca energía eléctrica) o sea pasivo (consuma energía eléctrica).
Terminología utilizada en el Estudio de los Circuitos
Para facilitar el estudio de un circuito conviene definir los siguientes términos:
- Nudos,
- Ramas
- y Mallas.
- Nudo es la unión de más de dos cables: Los puntos A y B son los dos únicos existentes en el circuito que se esquematiza debajo; el punto C es la unión de dos elementos, pero no es un nudo.
- Rama es el recorrido a lo largo del circuito entre dos nudos consecutivos: Una rama del circuito es ACB, pero no es una rama BAC. En el esquema se distinguen 3 ramas: ACB, BDA y AB.
- Malla es un recorrido cerrado. Por ejemplo ABDA (malla I) y ACBA (malla II). También lo es el recorrido exterior BDACB, pero es redundante con las anteriores (I y II) que ya cubren todos los elementos recorridos por la última
Previo a proceder al estudio de un circuito se identifican las corrientes que van por cada rama (también puede efectuarse el estudio en términos de las corrientes que circulan por las mallas).
En nuestro circuito podemos distinguir 3 corrientes diferentes: I1, I2 e I3. Observe que los nombres y los sentidos de las corrientes se asignan arbitrariamente; si, tras analizar el circuito, una corriente resulta negativa es que su sentido es opuesto al inicialmente escogido.
En nuestro circuito podemos distinguir 3 corrientes diferentes: I1, I2 e I3. Observe que los nombres y los sentidos de las corrientes se asignan arbitrariamente; si, tras analizar el circuito, una corriente resulta negativa es que su sentido es opuesto al inicialmente escogido.
Las reglas utilizadas para el estudio de un circuito son las llamadas Leyes de Kirchhoff: básicamente la ley de nudos y la ley de mallas que analizaremos posteriormente.
A la vista de lo expuesto anteriormente queremos resaltar que lo necesario para proceder al estudio de un circuito es conocer, para cada elemento o dispositivo que lo forme, la relación que hay entre la intensidad que atraviesa al dispositivo y la caída de potencial o voltaje entre sus extremos.
Esta relación suele darse en términos de la denominada característica I-V del dispositivo y esta primera práctica va orientado a mostrar dicha característica para diferentes dispositivos.
Característica I-V de un dispositivo
Esta característica informa sobre la relación que existe entre I y V en un dispositivo y constituye todo lo que hay que saber de un dispositivo para poder estudiar su comportamiento y efectos al insertarlo en un circuito dado. Esta relación puede presentarse en forma de tabla, dando pares de valores V-I. También puede presentarse en forma gráfica dando I como función de V o viceversa.
Baterías
Supondremos que los circuitos en que fijamos nuestra atención están alimentados por baterías ideales. Estas baterías tienen una característica V-I muy simple: dan un voltaje fijo (su f.e.m.) para cualquier valor de la corriente que se les pida. En forma gráfica tendríamos:
En este caso sería una pérdida de tiempo conservar la gráfica o una tabla de valores asociada a dicha característica, pues el único dato relevante es el valor de la f.e.m. Bien es verdad que la característica anteriormente expuesta es ideal, como hemos dicho: supone que la batería podría suministrar cualquier valor de corriente manteniendo la d.d.p. entre sus bornes, lo cual implicaría que podría suministrar potencias infinitas.
Resistencias
Otra característica sencilla es la que corresponde a elementos lineales como las resistencias. En estos dispositivos la corriente es linealmente proporcional a la tensión aplicada a sus extremos (o, a la inversa, el voltaje desarrollado entre los extremos del elemento es proporcional a la corriente que lo atraviesa):
En estas situaciones realmente hay un exceso de información y bastaría con dar la pendiente de la recta como representativa de toda la información. En este caso se cumple la ley de Ohm y el dispositivo se caracteriza por un único parámetro: la pendiente, R (en Ohmios), de la gráfica anteriormente representada:
Ley de Ohm: V=R.I
En la representación anterior la recta de mayor pendiente (en azul) corresponde a la resistencia, R, de mayor valor puesto que se ha presentado en diagrama donde la pendiente es V/I. Conviene destacar que frecuentemente se da la característica con los ejes intercambiados:
En los circuitos de corriente continua, puede resolverse la relación entre la corriente, voltaje, resistencia y potencia con la ayuda de un gráfico de sectores, este diagrama ha sido uno de los más socorridos:
Dispositivos No Lineales
En estos dispositivos la característica V-I no corresponde a una recta. Como ejemplos tipo veamos el Diodo y el Diodo Zener.
El Diodo
Un ejemplo representativo de elemento no lineal lo constituye el Diodo. Este dispositivo, utilizado, por ejemplo, para rectificar la corriente alterna
Este dispositivo se utiliza par estabilizar la tensión a un cierto valor de referencia. Su característica, idealmente, es como la siguiente:

El diodo presenta Resistencia cero cuando se polariza en Directo (V positiva) y resistencia infinita cuando se polariza en Inverso (V negativa)
El Diodo Zener
Este dispositivo se utiliza par estabilizar la tensión a un cierto valor de referencia. Su característica, idealmente, es como la siguiente:

La rama vertical de la izquierda significa que el diodo estabiliza a un potencial de referencia VREF no importa la intensidad que lo atraviese. VREF es un parámetro del diodo que puede seleccionarse en un amplio rango de valores.
Aparatos de Medida Eléctricos
Las magnitudes básicas a medir en un Circuito son la Intensidad de corriente y el Voltaje.
La medida de la Intensidad de corriente eléctrica se efectúa con aparatos denominados Amperímetros. La medida de diferencias de potencial o voltajes se efectúa con Voltímetros.
Los Amperímetros se intercalan en serie con los elementos incluidos en la rama donde se quiere medir qué corriente pasa.
Los Voltímetros se conectan en paralelo entre los puntos donde quiere medirse la d.d.p.
Para que un Amperímetro no altere el circuito en que se intercala ha de tener una resistencia interna muy baja, idealmente cero. Al contrario, para que un voltímetro no perturbe la medida debe tener una resistencia interna muy elevada, idealmente infinita.
Para que un Amperímetro no altere el circuito en que se intercala ha de tener una resistencia interna muy baja, idealmente cero. Al contrario, para que un voltímetro no perturbe la medida debe tener una resistencia interna muy elevada, idealmente infinita.
En ocasiones, cuando se dispone sólo de Voltímetros como aparato de medida, para medir corrientes puede intercalarse una pequeña resistencia (r) en la rama correspondiente y medir el voltaje (v) que cae en ella. La corriente resultante es: I= v/r.
Leyes de Kirchhoff para el análisis de los circuitos
Las leyes de Kirchhoff se utilizan para la resolución de un circuito en la forma que se expone a continuación. Utilizaremos como ejemplo de aplicación el circuito ya presentado anteriormente:
La ley de nudos proviene de la conservación de la carga y dice, esencialmente, que la suma de las corrientes que llegan a un nodo es cero; es decir, que el total de corriente que entra (signo mas, por ejemplo) es igual al total de la corriente que sale del nudo (signo menos en su caso).
Esta ley ha de aplicarse a tantos nudos existan en nuestro circuito, menos uno. En nuestro caso, a un nudo; seleccionando el nudo A y suponiendo definimos como positiva la corriente entrante en el nudo:
I1 - I2 - I3 = 0
La ley de mallas establece que la suma de caídas de potencial a lo largo de una malla debe coincidir con la suma de fuerzas electromotrices (de los elementos activos) a lo largo de la misma. Si no hubiera elementos activos, la suma de potenciales a lo largo de un recorrido cerrado es cero, lo cual está ligado al carácter conservativo del campo eléctrico. Para su aplicación es preciso previamente asignar un sentido de recorrido a las mallas y dar algún convenio de signos:
Una f.e.m se tomará como positiva si en nuestro recorrido salimos por el polo positivo. Una caída de potencial se tomará como positiva si en nuestro recorrido vamos a favor de la corriente cuando pasamos por el elemento. En nuestro circuito las caídas de potencial son todas en resistencias óhmicas; si es I la intensidad que atraviesa a una resistencia R, la caída de potencial es IR.
En nuestro caso, utilizando las mallas I y II recorridas en los sentidos indicados tendremos las siguientes ecuaciones:
e1 = I1R1 + I3R3
-e2 = I2R2+I2R4– I3R3 = I2(R2 + R4) – I3R3
Conocidos los valores de los elementos que constituyen nuestro circuito, las tres ecuaciones anteriormente expuestas configuran un sistema lineal del que se pueden despejar los valores de I1, I2 e I3. Obsérvese que en el circuito anterior R2 y R4 se asocian como si fueran una sola resistencia de valor (R2 + R4).
Este es un ejemplo de cómo se asocian resistencias en serie, que son las que están en una misma rama no importando en qué ubicación.
Este es un ejemplo de cómo se asocian resistencias en serie, que son las que están en una misma rama no importando en qué ubicación.
Asociación de elementos en Serie y en Paralelo
Previo a analizar un circuito conviene proceder a su simplificación cuando se encuentran asociaciones de elementos en serie o en paralelo.
El caso estudiado anteriormente corresponde, como se ha dicho, a una asociación de resistencias en Serie. Se dice que varios elementos están en serie cuando están todos en la misma rama y, por tanto, atravesados por la misma corriente.
El caso estudiado anteriormente corresponde, como se ha dicho, a una asociación de resistencias en Serie. Se dice que varios elementos están en serie cuando están todos en la misma rama y, por tanto, atravesados por la misma corriente.
Si los elementos en serie son Resistencias, ya se ha visto que pueden sustituirse, independiente de su ubicación y número, por una sola resistencia suma de todas las componentes.
En esencia lo que se está diciendo es que la dificultad total al paso de la corriente eléctrica es la suma de las dificultades que individualmente presentan los elementos componentes
Esta regla particularizada para el caso de Resistencias sirve también para asociaciones de f.e.m. (baterías).
Por otra parte, se dice que varios elementos están en Paralelo cuando la caida de potencial entre todos ellos es la misma. Esto ocurre cuando sus terminales están unidos entre si como se indica en el esquema siguiente
Ahora la diferencia de potencial entre cualquiera de las resistencias es V, la existente entre los puntos A y B. La corriente por cada una de ellas es V/Ri (i=1,2,3) y la corriente total que va de A a B (que habría de ser la que atraviesa Rp cuando se le aplica el mismo potencial) será I1 + I2 + I3. Para que esto se cumpla el valor de la conductancia 1/Rp ha de ser la suma de las conductancias de las Resistencias componentes de la asociación:
1/Rp = 1/R1 + 1/R2 + 1/R3
Lo cual significa que, al haber tres caminos alternativos para el paso de la corriente, la facilidad de paso (conductancia) ha aumentado: la facilidad total es la suma de las facilidades.
Las baterías No suelen asociarse en paralelo, debido a su pequeña resistencia interna. Si se asociaran tendrían que tener la misma f.e.m. que sería la que se presentaría al exterior. Pero cualquier diferencia daría lugar a que una de las baterías se descargara en la otra.
Figura. Disposición de bombillas en un circuito en serie y un circuito en paralelo.
Potencia eléctrica.
Al circular la corriente, los electrones que la componen colisionan con los atomos del conductor y ceden energía, que aparece en la forma de calor. La cantidad de energía desprendida en un circuito se mide en julios. La potencia consumida se mide en vatios; 1 vatio equivale a 1 julio por segundo. La potencia "P" consumida por un circuito determinado puede calcularse a partir de la expresión:
 (9)
(9)
Donde:
V: diferencia de potencial o voltaje aplicado a la resistencia, Voltios
I: corriente que atraviesa la resistencia, Amperios
R: resistencia, Ohmios
P: potencia eléctrica, Watios
Para cuantificar el calor generado por una resistencia eléctrica al ser atravesada por una corriente eléctrica, se usa el siguiente factor de conversión:
1 Watt = 0,2389 calorías / segundo
Regla del divisor de tensión.
Al circular la corriente, los electrones que la componen colisionan con los atomos del conductor y ceden energía, que aparece en la forma de calor. La cantidad de energía desprendida en un circuito se mide en julios. La potencia consumida se mide en vatios; 1 vatio equivale a 1 julio por segundo. La potencia "P" consumida por un circuito determinado puede calcularse a partir de la expresión:
 (9)
(9)Donde:
V: diferencia de potencial o voltaje aplicado a la resistencia, Voltios
I: corriente que atraviesa la resistencia, Amperios
R: resistencia, Ohmios
P: potencia eléctrica, Watios
Para cuantificar el calor generado por una resistencia eléctrica al ser atravesada por una corriente eléctrica, se usa el siguiente factor de conversión:
1 Watt = 0,2389 calorías / segundo
Regla del divisor de tensión.
La evaluación de la tensión que pasa por cualquier resistor o cualquier combinación de resistores en un circuito en serie se puede reducir a un solo elemento utilizando la regla del divisor de tensión. La prueba, que es muy corta y directa, se desarrollará con el circuito de la Figura 4.

Figura 4. Circuito en serie donde la corriente I atraviesa todos los resistores sin sufrir derivación alguna
a) Resistencia total: Rt = R1 + R2 + R3 +…RN (12)
b) Corriente: I = V/RT (13)
C) Tensión a través del resistor RX (donde x puede ser cualquier número de 1 a N): Vx = I.Rx
D) La tensión a través de dos o más resistencias en serie que tienen una resistencia total igual a:
R’T: V’T = I.RT (14)
E) Se sustituye I del inciso (B) en las ecuaciones de los incisos (C) y (D):
Regla del divisor de tensión:
 (15)
(15) (16)
(16)En palabras, la regla indica que, para un circuito en serie, la tensión que existe en cualquier resistor (o alguna combinación de resistores en serie) es igual al valor de ese resistor (o a la suma de dos o más resistores en serie) multiplicado por la diferencia de potencial de todo el circuito en serie y dividido entre la resistencia total del circuito. Obsérvese que no es necesario que V sea una fuente de fuerza electromotriz.
Para dos derivaciones paralelas, la corriente que pasa por cualquier derivación es igual al producto del otro resistor en paralelo y la corriente de entrada dividido entre la suma de los dos resistores en paralelo (Figura 5).
 (17)
(17) (18)
(18)
Figura 5. Circuito en paralelo donde la corriente IT atraviesa todos los resistores pero sufriendo una derivación.
Conversión de fuentes de tensión a fuentes de corriente y viceversa.
La fuente de corriente es el dual de la fuente de tensión. El término dual indica que lo que sea característico de la tensión o la corriente de una batería lo será también para la corriente o la tensión, según el caso, de una fuente de corriente. La fuente de corriente proporciona una corriente fija a la derivación en que está situada, mientras que su tensión final puede variar como lo determine la red a la que se aplica.
Durante la conversión, el valor de la resistencia que se encuentre en paralelo con la fuente de tensión tendrá el mismo valor que la resistencia ubicada en paralelo con la fuente de corriente, no obstante, la corriente proporcionada por la fuente de corriente se relaciona con la fuente tensión a través de:
 (21)
(21)Por último, la dirección de la corriente quedará establecida en función de la polaridad de la fuente de tensión, pues siempre saldrá de la terminal positiva (Figura 6).

Figura 6. Una fuente de tensión es convertida en una fuente de corriente. La resistencia que se encuentra en serie con la fuente de tensión (RTh) conserva su valor, pero aparece en paralelo con la fuente de corriente, mientras que la corriente IN resulta de dividir ETh con RTh. Su sentido siempre será ubicado a la salida de la terminal positiva (el bigote más grande de la fuente).
Análisis de circuitos por el método de las mallas.
El siguiente método de formato es usado para abordar el análisis de mallas.
1Asignar una corriente de malla a cada trayectoria cerrada independiente en el sentido de las manecillas del reloj (Figura 7).
2. El número de ecuaciones necesarias es igual al número de trayectorias cerradas independientes escogidas. La columna 1 de cada ecuación se forma sumando los valores de resistencia de los resistores por los que pasa la corriente de malla que interesa y multiplicando el resultado por esa corriente de malla.
3. Debemos considerar los términos mutuos, se restan siempre de la primera columna. Es posible tener más de un término mutuo si la corriente de malla que interesa tiene un elemento en común con más de otra corriente de malla. Cada término es el producto del resistor mutuo y la otra corriente de malla que pasa por el mismo elemento.
4. La columna situada a la derecha del signo igual es la suma algebraica de las fuentes de tensión por las que pasa la corriente de malla que interesa. Se asignan signos positivos a las fuentes de fuerza electromotriz que tienen una polaridad tal que la corriente de malla pase de la terminal negativa a la positiva. Se atribuye un signo negativo a los potenciales para los que la polaridad es inversa.
5. Se resuelven las ecuaciones simultáneas resultantes para las corrientes de malla deseadas.
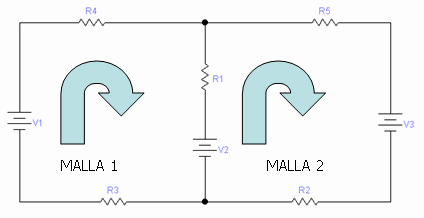
Figura 7. Una red eléctrica donde claramente se distinguen dos mallas. Nótese como las corrientes de malla se dibujan en el sentido de las agujas del reloj.
El siguiente método de formato es usado para abordar el análisis nodal
1. Escoger un nodo de referencia y asignar un rótulo de voltaje con subíndice a los (n — 1) nodos restantes de la red (Figura 8).
2. El número de ecuaciones necesarias para una solución completa es igual al número de tensiones con subíndice (N - 1). La columna 1 de cada ecuación se forma sumando las conductancias ligadas al nodo de interés y multiplicando el resultado por esa tensión nodal con subíndices.
3. A continuación, se deben considerar los términos mutuos, se restan siempre de la primera columna. Es posible tener más de un término mutuo si la tensión nodal de la corriente de interés tiene un elemento en común con más de otra tensión nodal. Cada término mutuo es el producto de la conductancia mutua y la otra tensión nodal enlazada a esa conductancia.
4. La columna a la derecha del signo de igualdad es la suma algebraica de las fuentes de corriente ligadas al nodo de interés. A una fuente de corriente se le asigna un signo positivo si proporciona corriente a un nodo, y un signo negativo si toma corriente del nodo.

Figura 8. Una red eléctrica donde claramente se distinguen cuatro nodos. Nótese como uno de los nodos se tomó como referencia, o sea, su potencial es cero.
5. Resolver las ecuaciones simultáneas resultantes para las tensiones nodales deseadas.
Con frecuencia se encuentran configuraciones de circuitos en que los resistores no parecen estar en serie o en paralelo.
Es esas condiciones, puede ser necesario convertir el circuito de una forma a otra para resolver variable eléctrica desconocida.
Dos configuraciones de circuitos que suelen simplificar esa dificultad son las transformaciones ye (Y) y delta (Δ), que se muestra en la Figura 9.

Figura 9. A la izquierda de la imagen se observa una configuración de resistencias en delta, a la derecha se presenta una configuración en ye.
Las relaciones entre ambas configuraciones son:
 (22)
(22) (23)
(23) (24)
(24) (25)
(25) (26)
(26) (27)
(27)El teorema establece que:
"La corriente o la tensión que existe en cualquier elemento de una red lineal bilateral es igual a la suma algebraica de las corrientes o las tensiones producidas independientemente por cada fuente"
Considerar los efectos de cada fuente de manera independiente requiere que las fuentes se retiren y reemplacen sin afectar al resultado final. Para retirar una fuente de tensión al aplicar este teorema, la diferencia de potencia entre los contactos de la fuente de tensión se debe ajustar a cero (en corto); el retiro de una fuente de corriente requiere que sus contactos estén abiertos (circuito abierto).
Cualquier conductancia o resistencia interna asociada a las fuentes desplazadas no se elimina, sino que todavía deberá considerarse.
La corriente total a través de cualquier porción de la red es igual a la suma algebraica de las corrientes producidas independientemente por cada fuente; o sea, para una red de dos fuentes, si la corriente producida por una fuente sigue una dirección, mientras que la producida por la otra va en sentido opuesto a través del mismo resistor, la corriente resultante será la diferencia entre las dos y tendrá la dirección de la mayor. Si las corrientes individuales tienen el mismo sentido, la corriente resultante será la suma de dos en la dirección de cualquiera de las corrientes.
Esta regla es cierta para la tensión a través de una porción de la red, determinada por las polaridades y se puede extender a redes con cualquier número de fuentes.
El principio de la superposición no es aplicable a los efectos de la potencia, puesto que la pérdida de potencia en un resistor varía con el cuadrado (no lineal) de la corriente o de la tensión. Por esta razón, la potencia en un elemento no se puede determinar sino hasta haber establecido la corriente total (o la tensión) a través del elemento mediante la superposición.
Las etapas a seguir que conducen al valor apropiado de RTH y ETH son:
1. Retirar la porción de la red a través de la cual se debe encontrar el circuito equivalente de Thevenin.
2. Marcar las terminales de la red restante de dos terminales (la importancia de esta etapa será evidente conforme examinemos algunas redes complejas).
3. Calcular RTH ajustando primero todas las fuentes a cero (las fuentes de tensión se reemplazan con circuitos en corto y las de corriente con circuitos abiertos) y luego determinar la resistencia resultante entre las dos terminales marcadas. (Si la resistencia interna de las fuentes de tensión y/o de corriente se incluye en la red original, deberá permanecer cuando las fuentes se ajusten a cero.)
4. Calcular ETH reemplazando primero las fuentes de corriente y de tensión, y determinando luego la tensión del circuito abierto entre las terminales marcadas. (Esta etapa será siempre la que conducirá a más confusiones y errores. En todos los casos debe recordarse que es el potencial de circuito abierto entre las dos terminales marcadas en la segunda etapa.)
5. Trazar el circuito equivalente de Thevenin reemplazando la porción del circuito que se retiró previamente, entre las terminales del circuito equivalente. Esta etapa se indica mediante la colocación del resistor R entre las terminales del circuito equivalente de Thevenin.
El Teorema de Norton al igual que el Teorema de Thevenin es un método empleado para evaluar el efecto de un red sobre una resistencia de carga. Esta técnica es aplicable a redes electrizas que poseen fuentes de corriente no variable. El teorema establece:
"Cualquier red lineal bilateral de c.d de dos terminales se puede reemplazar con un circuito equivalente que consiste en una fuente de corriente y un resistor en paralelo"
El análisis del teorema de Thevenin con respecto al circuito equivalente se puede aplicar también al circuito equivalente de Norton.
Las etapas que conducen a los valores apropiados de IN Y RN son:
1. Retirar la porción de la red en que se encuentra el circuito equivalente de Norton.
2. Marcar las terminales de la red restante de dos terminales.
3. Calcular RN ajustando primero todas las fuentes a cero (las fuentes de tensión se reemplazan con circuitos en corto y las de corriente con circuitos abiertos) y luego determinando la resistencia resultante entre las dos terminales marcadas. (Si se incluye en la red original la resistencia interna de las fuentes de tensión y/o corriente, ésta deberá permanecer cuando las fuentes se ajusten a cero.)
4. Calcular IN reemplazando primero las fuentes de tensión y de corriente, y encontrando la corriente a circuito en corto entre las terminales marcadas.
5. Trazar el circuito equivalente de Norton con la porción previamente retirada del circuito y reemplazada entre las terminales del circuito equivalente.

R1 R2 R3 R4 Voltaje(V) 50 50 50 50 Corriente(mA) 1000 50 16,67 4,995 Potencia(W) 50 2,5 0,8335 0,24975
- Rellene el siguiente cuadro con el voltaje, la corriente y la potencia eléctrica disipada por cada resistor.

R1 R2 R3 Voltaje(V) 16 16 48 Corriente(A) 1.333 2.667 4.000 Potencia(W) 0,0213280,0426720,192- Rellene el siguiente cuadro con el voltaje, la corriente y la potencia eléctrica disipada por cada resistor:

R1 R2 R3 R4 Voltaje(V) 2.807.004.204.20Corriente(mA) 14001400700700Potencia(W) 3,929,82,942,94 - Calcule la diferencia de potencial entre a y b, así como la corriente, el voltaje y la potencia consumida por cada resistor: Sol. 0,001 V

R1 R2 R3 R4 R5 R6 R8 Voltaje(V) 0.0074 0.0065 0.1383 0.1383 0.1383 0.1383 14.99 Corriente(mA) 2.306 2.306 3.458 3.458 2.306 3.458 14.99 Potencia(W) 0,01706440,0149890,47824140,47824140,31891980,47824140,2247001 - Rellene el siguiente cuadro con el voltaje, la corriente y la potencia eléctrica disipada por cada resistor:
R1 R2 R3 Voltaje(V) 0.2502.2509.750Corriente (mA) 62.50750812.5Potencia(W) 0,0156251,68757,921875- Determine la corriente, el voltaje y la potencia que consume cada resistor en la red mostrada:

| Resistencia () | 7 | 3 | 4 | 2 | 8 | 20 | 1 | 1.5 |
| Voltaje(V) | 3,3285 | 0,14763 | 2,0988 | 0,5726 | 3,7536 | 4,616 | 0,1892 | 0,630 |
| Corriente (mA) | 475,5 | 49,21 | 524,7 | 286,3 | 469,2 | 230,8 | 189,2 | 420 |
| Potencia(W) | 1,5827 | 0,0073 | 1,1012 | 0,1639 | 1,7612 | 1,0654 | 0,0358 | 0,2646 |
- Determine la corriente, el voltaje y la potencia consumida por cada resistor en la red presentada a continuación:
- Un calefactor por radiación, de 1250 W, se fabrica de tal forma que opera a 115 V. ¿Cuál será la corriente en el calefactor?.¿cual será la resistencia de la bobina calefactora?. ¿Cuántas kilocalorías irradia el calefactor en una hora? Sol. 11 A; 11 ; 1100 Kcal

- Calcule el circuito equivalente Norton del resistor de 4 . Sol. 6,7 ; 10,75 A (de arriba hacia abajo)

- Calcule el circuito equivalente Thevenin del resistor de 2 Ώ . Sol. 5,65 ; 13,043 V
- Aplicando el teorema de Superposición calcúlese la corriente que pasa por el resistor de 10 . Sol. 523,7 mA
- En un circuito en serie simple circula una corriente de 5 A. Cuando se añade una resistencia de 2 W en serie, la corriente decae a 4 A. ¿Cuál es la resistencia original del circuito?. Sol. 8
- Una resistencia de 0,10 W debe generar energía térmica con un ritmo de 10 W al conectarse a una batería cuya fem es de 1,5 V. ¿Cuál es la resistencia interna de la batería?. ¿Cuál es la diferencia de potencial que existe a través de la resistencia?. Sol. 0,050 ; 1,0 V
- Doce resistencias, cada una de resistencia R, se interconectan formando un cubo. Determinar la resistencia equivalente RAB de una arista. Calcular la resistencia equivalente RBC de la diagonal de una de las caras. Determinar la resistencia equivalente RAC de una diagonal del cubo. Sol. 7/12 R; ¾ R; 5/6 R
PREGUNTAS DE RAZONAMIENTO
- Dos lámparas incandescentes, una de 500 W y otra de 100 W, operan a 110 V. ¿Cuál de las dos lámparas tiene menor resistencia?
- ¿Depende el sentido de la fem suministrada por una batería del sentido en el cual fluye la corriente a través de la batería?
- Describir un método para medir la fem y la resistencia interna de una batería.
- Una lámpara incandescente de 110 V, 25 W, brilla normalmente cuando se conecta a través de un conjunto de baterías. Sin embargo, otra lámpara incandescente de 110 V, 500 W brilla solo levemente al conectarse a través del mismo conjunto. Explicar el hecho.
- ¿Cuál es la diferencia entre la fem y la diferencia de potencial?
- ¿En que circunstancias puede la diferencia de potencial terminal de una batería exceder a su fem?
- Explicar por qué debe ser muy pequeña la resistencia de un amperímetro, en tanto que la de un voltímetro debe ser muy grande.
- ¿Cuál es la diferencia entre resistencia y resistividad?
- ¿Qué se requiere para mantener una corriente estable en un conductor?
- ¿Qué factores afectan la resistencia de un conductor?
- Dos focos eléctricos operan a 110 V, pero uno tiene un valor nominal de potencia de 25 W y el otro de 100 W. ¿Cuál de los focos tiene la resistencia más alta?. ¿Cuál de ellos conduce la mayor corriente?
- ¿Cómo podría Ud. conectar resistores de manera que la resistencia equivalente sea más pequeña que las resistencias individuales?
- ¿Cuándo puede ser positiva la diferencia de potencial a través de un resistor?
- Una lámpara incandescente conectada a una fuente de 120 V con un cordón de extensión corto brinda más iluminación que la misma conectada a la misma fuente con un cordón de extensión muy largo. Explique.

R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 Voltaje(V) Corriente(A) Potencia(W) - Rellene el siguiente cuadro con el voltaje, la corriente y la potencia eléctrica disipada por cada resistor:
- Un conductor coaxial con una longitud de 20 m está compuesto por un cilindro interior con un radio de 3 mm y un tubo cilíndrico exterior concéntrico con un radio interior de 9 mm. Una corriente de fuga de 10 A fluye entre los dos conductores. Determine la densidad de la corriente de fuga (en A/m2) a través de una superficie cilíndrica (concéntrica con los conductores) que tiene un radio de 6 mm.
- Un conductor de 1,2 cm de radio conduce una corriente de 3 A producida por un campo eléctrico de 120 V/m. ¿Cuál es la resistividad del material?
- Un campo electrico de 2100 V/m se aplica a un trozo de plata de sección transversal uniforme. Calcule la densidad de corriente resultante si la muestra está a una temperatura de 20 ºC.

R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 Voltaje(V) Corriente(A) Potencia(W) - Rellene el siguiente cuadro con el voltaje, la corriente y la potencia eléctrica disipada por cada resistor:
- Un alambre metálico de 12 se corta en tres pedazos iguales que luego se conectan extremo con extremo para formar un nuevo alambre, cuya longitud es igual a la tercera parte de la longitud original. ¿Cuál es la resistencia de este nuevo alambre?
- Se encuentra que alambres de aluminio y cobre de igual longitud tiene la misma resistencia. ¿Cuál es la proporción de sus radios?
- Un resistor se construye con una barra de carbón que tiene un área de sección transversal uniforme de 5 mm2. Cuando una diferencia de potencial de 15 V se aplica entre los extremos de la barra. Encuentre: la resistencia de la barra y su longitud.
- ¿Cuál es el cambio fraccionario de la resistencia de un filamento de hierro cuando su temperatura cambia de 25 ºC a 50 ºC?

R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 Voltaje(V) Corriente(mA) Potencia(mW) - Rellene el siguiente cuadro con el voltaje, la corriente y la potencia eléctrica disipada por cada resistor:
- Una batería tiene una fem de 15 V. El voltaje terminal de la batería es de 11,6 V cuando ésta entrega 20 W de potencia a un resistor de carga externo R. ¿Cuál es el valor R?. ¿Cuál es la resistencia interna de la batería?
- ¿Qué diferencia de potencial se mide a través de un resistor de carga de 18 que se conecta a una batería de 5 V de fem y una resistencia interna de 0,45 ?
- La corriente en un circuito se triplica conectando un resistor de 500 en paralelo con la resistencia del circuito. Determine la resistencia del circuito en ausencia del resistor de 500 .
- Cuando dos resistores desconocidos se conectan en serie con una batería, se disipa 225 W con una corriente total de 5 A. Para la misma corriente total, se disipa 50 W cuando los resistores se conectan en paralelo. Determine los valores de los dos resistores.

R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 Voltaje(V) Corriente(mA) Potencia(W) - Rellene el cuadro con las variables eléctricas pedidas:
- Se cuenta con una esfera conductora de 10 cm de radio hacia la cual se hace circular una corriente de 1,0000020 A mediante un alambre, en tanto otro alambre extrae de ella una corriente de 1,0000000 A. ¿Cuánto tiempo transcurre antes de que la esfera aumente su potencial a 1000 V?
- Un resistor tiene forma de cono circular recto truncado. Los radios de los extremos son a y b y la altura L. Si la abertura del cono es pequeña, puede suponerse que la densidad de corriente es uniforme a través de cualquier área transversal. Calcular la resistencia de éste objeto.
- En un alambre de calibre 18 (diámetro = 0,040 pulgadas) y 100 pies de longitud se aplica una diferencia de potencial de 1 V. Calcular: la corriente, la densidad de corriente, el campo eléctrico, y el ritmo con que se genera energía térmica en el alambre.
- Se desea fabricar un conductor cilíndrico largo cuyo coeficiente térmico de resistividad a 20 º C tenga un valor cercano a cero. Si este conductor se hace alternando discos de hierro y de carbón, ¿Cuál debe ser la relación de los espesores de los discos de carbón a los de hierro?. Supóngase que la temperatura permanece constante igual en todos los discos. ¿Cuál debe ser la relación de la energía térmica generada en el disco de carbón al disco de hiero?

R1 R2 R3 R4 R5 R6 R7 R8 R9 R10 Voltaje(V) Corriente(mA) Potencia(W) - Rellene el cuadro con las variables eléctricas pedidas:

R1 R2 R3 R4 R5 R6 Voltaje(V) Corriente(A) Potencia(W) - Rellene el siguiente cuadro con el voltaje, la corriente y la potencia eléctrica disipada por cada resistor:

- Obténgase las corrientes de mallas del siguiente circuito:
- Una batería de automóvil (12 V) tiene una carga inicial Q (120 A.h). Suponiendo que el potencial a través de las terminales permanece constante hasta que la batería se descargue totalmente, ¿durante cuantas horas puede suministrar una potencia P (100 W)?

- Obténgase las corrientes de mallas del siguiente circuito:
R1 R2 R3 R4 R5 R6 R7 R8 R9 Voltaje(V) Corriente(A) Potencia(W) 
- Rellene el siguiente cuadro con el voltaje, la corriente y la potencia eléctrica disipada por cada resistor:
- Cuando una barra de metal se calienta, cambia no solo su resistencia, sino también su longitud y el área de su sección transversal. La relación:
 , sugiere que deben tomarse en cuenta los tres factores al medir r a diversas temperaturas. Si la temperatura cambia 1 ºC, ¿qué tanto por ciento cambian: R, L y A para un conductor de cobre?. ¿Qué conclusión saca usted?. El coeficiente de dilatación térmica lineal del cobre es de 1,7 x 10-5 ºC-1.
, sugiere que deben tomarse en cuenta los tres factores al medir r a diversas temperaturas. Si la temperatura cambia 1 ºC, ¿qué tanto por ciento cambian: R, L y A para un conductor de cobre?. ¿Qué conclusión saca usted?. El coeficiente de dilatación térmica lineal del cobre es de 1,7 x 10-5 ºC-1. - Un tostador de 1000 W, un horno de microonda de 800 W y una cafetera de 500 W se conectan en el mismo tomacorriente de 120 V. Si el circuito se protege por medio de un fusible de 20 A. ¿se fundirá el fusible si todos los aparatos se usan al mismo tiempo?
- Un cordón de 8 pies de extensión tiene dos alambres de cobre de calibre 18, cada uno con un diámetro de 1,024 mm. ¿Cuánta potencia disipa este cordón cuando conduce una corriente de: 1 A y 10 A.

- Determine el voltaje en la resistencia de 12 Kilo-ohmios:
- Una compañía eléctrica emplea dos rollos de 50 m cada uno de alambre de cobre para enganchar, desde el tendido general, el local de un abonado. La resistencia eléctrica del hilo es de 0,3 cada 1000 m. Calcular la caída de tensión en la línea estimando en 120 A de c.c. (corriente continua) la intensidad de carga.

- Calcúlese la potencia disipada por el resistor de 5 k.
- Un galvanómetro que tiene una sensibilidad de máxima escala de 1 mA requiere un resistor en serie de 900 W para efectuar una lectura de máxima escala del voltímetro cuando se mide 1 V en las terminales. ¿Qué resistor en serie se requiere para convertir el mismo galvanómetro en un voltímetro de 50 V (máxima escala)?

- En el circuito adjunto determine la tensión en el resistor de 35 kilo-ohmios:

- En el circuito adjunto se sabe que la potencia consumida por el resistor de 15 kilo-ohmio es igual a 125 W. ¿Cuánto valdrá V?.

- En el circuito adjunto determine la tensión en el resistor de 25 kilo-ohmios:

- En el circuito adjunto se sabe que la potencia consumida por el resistor de 65 kilo-ohmio es igual a 250 W. ¿Cuánto valdrá V?
- Determine en la potencia disipada por el resistor de 130 kilo-ohmios:
- En el circuito mostrado determine: voltaje, corriente y potencia disipada por el resistor de 64 k.

Alonso, M. y Finn, E. (1986) Física. Volumen II: Mecánica. Addison – Wesley Iberoamericana.
Resnick, R. y Halliday, D. (1984) Física. Tomo II (séptima impresión). Compañía Editorial Continental: México.
Serway, Raymond (1998) Física. Tomo II (Cuarta edición). Mc Graw-Hill: México.



